Sommige redeneringen bestaan uit meer dan slechts twee premissen of uit meerdere combinaties van de premissen. Als je de waarheid van een dergelijke redenering wil bepalen heb je een grotere waarheidstafel nodig, tenminste als je de propositielogica gebruikt met de bijhorende taal.
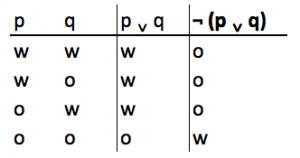
Stel je voor dat je de geldigheid van de formule ¬(p ∨ q) moet bepalen. Dan ziet de waarheidstafel er als volgt uit:
De eerste twee kolommen bevat de basiswaarheidstafel zoals wij deze al kennen. De derde kolom voegt iets toe, namelijk de negatie van p ∨ q. Met behulp van de negatie ‘¬‘ kunnen wij vanuit de tweede kolom ‘p ∨ q‘, de derde ‘¬(p ∨ q)‘ maken. Uit de waarheidstafel blijkt dat ¬(p ∨ q) alleen geldig is wanneer premisse p en premisse q onwaar is.
Nog een ander voorbeeld. Laten wij de geldigheid bepalen van ‘¬p ∨ (q ∧ r)‘. Allereerst moet opvallen dat er een premisse bij is gekomen, naast premisse p en premisse q zien wij premisse r. Allereerst bepalen wij de basis voor p, q en r. Aan de hand daarvan bepalen wij ¬p en (q ∧ r). Als laatste kijken wij naar de hele redenering ¬p ∨ (q ∧ r).
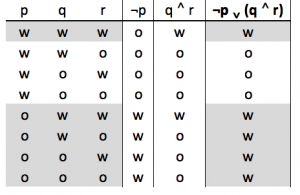
De eerste drie kolommen (p, q, r) geven de mogelijke waarheidswaarde aan van de premisse. De vierde kolom geeft de geldigheidswaarde aan van ¬p; dit is een basis waarheidstafel. De vijfde kolom geeft de geldigheidswaarde aan van q ∧ r; dit is een basis waarheidstafel. Ten slotte geeft de laatste kolom aan wat de geldigheidswaarde is van de hele redenering ¬p ∨ (q ∧ r); dit is een afgeleide van de kolom ¬p en de kolom (q ∧ r). Op de rijen waar een ‘w’ staat is de redenering geldig. Deze is grijs gemarkeerd. Dit betekent dat de hele redenering ¬p ∨ (q ∧ r) geldig is wanneer;
- p, q en r allen waar zijn
- p alleen onwaar is, en p en r beide waar zijn.
- p en r beide onwaar zijn en q waar is.
- p en q beide onwaar zijn en r waar is.
- p, q en r onwaar zijn.
Op deze manier kun je elk mogelijke combinatie van de premissen p, q en r. Je kunt namelijk vanuit de basis van de waarheidstafels alle andere combinaties samenstellen. Nog een voorbeeld p ↔ ( q → ¬ r ).
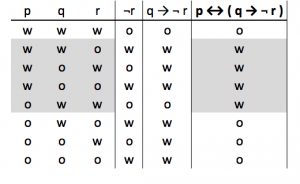
De eerste drie kolommen geven de mogelijke waarheidswaarde van p, q en r aan. De vierde kolom geeft de waarheidswaarde van ¬ r aan; dit is een basis waarheidstafel. De vijfde kolom geeft de geldigheid aan van q → ¬ r; dit is een afgeleide van de kolom ¬ r en de kolom q. De laatste kolom laat de geldigheid zien van de hele redenering p ↔ ( q → ¬ r ); dit is een afgeleide van de kolom p en de kolom ( q → ¬ r ).
De rijen die grijs gemarkeerd zijn, die een ‘w’ bevat, zijn de geldige redeneringen. De redenering p ↔ ( q → ¬ r ) is alleen geldig als;
- p en q beide waar zijn en r alleen onwaar is.
- p en r beide waar zijn en q alleen onwaar is.
- p alleen waar is, en q en r beide onwaar zijn.
- p alleen onwaar is, en q en r beide waar zijn.
Vanuit de natuurlijke taal kun je door middel van formele taal de geldigheid van een redenering testen. De positielogica is daar slechts een van de manieren van. Wij kennen ook andere logica vormen zoals de predikatenlogica.