Binnen de propositielogica gaan wij de geldigheid van een argumentatie na. Voordat wij de geldigheid na kunnen gaan moet de natuurlijke taal eerst omgezet worden naar formele taal met logische constanten en hulptekens. Wij hebben al vastgesteld dat een redenering logisch geldig is als de conclusie noodzakelijk volgt uit de premissen. Door middel van waarheidstafels gaan wij na of dit het geval is bij een argumentatie.
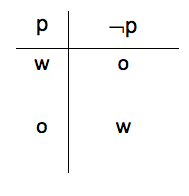
Voorbeeld van een waarheidstafel bij de logische constante ¬:
In het tabel zie je in de linker kolom onder ‘p’ een ‘w’ of een ‘o’ staan. De ‘w’ staat voor waar en de ‘o’ staat voor onwaar. Rechts staat hetzelfde onder ‘¬p’. De waarheidstafel geeft aan als ‘p’ waar is ‘w’, dan is ‘¬p‘ onwaar oftewel ‘o’. Als ‘p’ waar is, dan is ‘¬p‘ onwaar. Als je stelt dat p = het regent, dan is ¬p = het regent niet.
∧
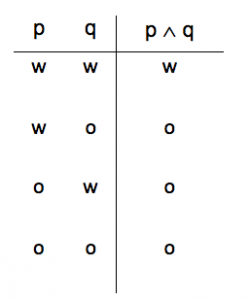
Voor elke logische constante is er een andere waarheidstafel. Dus ook voor de logische constante ‘∧’, en. In het voorbeeld is p = het regent en q = de straat is nat, de uitspraak is dus ‘het regent en straat is nat‘:
- Hier staat in de eerste regel dat ‘p ∧ q’ alleen waar ‘w’ is als zowel ‘p’ als ‘q’ afzonderlijk ook waar ‘w’ zijn. Dus het regent en de straat is nat. De hele premisse is waar als beide variabelen waar zijn.
- In de tweede regel staat dat ‘p ∧ q’, het regent en de straat is nat, onwaar is wanneer ‘p’ waar is en ‘q’ onwaar. Dus ‘p ∧ q’ is onwaar als het wel regent en de straat niet nat is. Als één variabele onwaar is, dan is de hele premisse onwaar.
- In de derde regel staat dat ‘p ∧ q’, het regent en de straat is nat, onwaar is wanneer ‘p’ onwaar is en ‘q’ waar. Dus ‘p ∧ q’ is onwaar als het niet regent en de straat nat is. Als één variabele onwaar is, dan is de hele premisse onwaar.
- In de vierde regel staat dat ‘p ∧ q’, het regent en de straat is nat, onwaar is wanneer zowel ‘p’ als ‘q’ onwaar is. Dus ‘p ∧ q’ is onwaar als het niet regent en de straat niet nat is. Als beide variabelen onwaar zijn, dan is de hele premisse onwaar.
∨
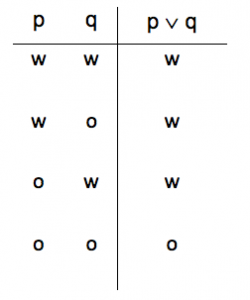
De waarheidstafel voor de logische constante ‘∨’, of, ziet er weer anders uit. In het voorbeeld is p = het regent en q = de straat is nat, de uitspraak is dus ‘het regent of straat is nat‘:
- Hier staat in de eerste regel dat ‘p ∨ q’ waar ‘w’ is als zowel ‘p’ als ‘q’ afzonderlijk ook waar ‘w’ zijn. Dus het regent of de straat is nat. Als ze beiden waar zijn, dan is de hele premisse ook waar.
- In de tweede regel staat dat ‘p ∨ q’, het regent of de straat is nat, waar is wanneer ‘p’ waar is en ‘q’ onwaar. Dus ‘p ∨ q’ is waar als het wel regent of de straat niet nat is. Slechts één variabele hoeft hiervoor waar te zijn.
- In de derde regel staat dat ‘p ∨ q’, het regent of de straat is nat, waar is wanneer ‘p’ onwaar is en ‘q’ waar. Dus ‘p ∨ q’ is waar als het niet regent of de straat nat is. Slechts één variabele hoeft hiervoor waar te zijn.
- In de vierde regel staat dat ‘p ∨ q’, het regent of de straat is nat, onwaar is wanneer zowel ‘p’ als ‘q’ onwaar is. Dus ‘p ∨ q’ is onwaar als het niet regent of de straat niet nat is. Als beide variabelen onwaar zijn, is de hele premisse onwaar.
↔
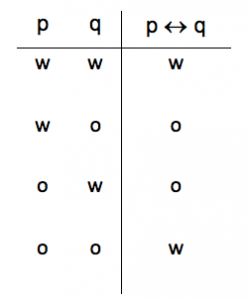
De waarheidstafel voor de logische constante ‘↔’, dan en slechts dan alleen. In het voorbeeld is p = het regent en q = de straat is nat, de uitspraak is dus ‘het regent dan en slechts dan als straat nat is‘:
- Hier staat in de eerste regel dat ‘p ↔ q’ waar ‘w’ is als zowel ‘p’ als ‘q’ afzonderlijk ook waar ‘w’ zijn. Dus het regent dan en slechts dan als de straat nat is. Als ze beiden waar zijn, dan is de hele premisse ook waar.
- In de tweede regel staat dat ‘p ↔ q’, het regent dan en slechts dan als de straat nat is, onwaar is wanneer ‘p’ waar is en ‘q’ onwaar. Dus ‘p ↔ q’ is onwaar als het wel regent en de straat niet nat is. Als de variabelen niet dezelfde waarheidswaarde hebben, dan is de hele premisse onwaar.
- In de derde regel staat dat ‘p ↔ q’, het regent dan en slechts dan als de straat nat is, waar is wanneer ‘p’ onwaar is en ‘q’ waar. Dus ‘p ↔ q’ is waar als het niet regent en de straat nat is. Als de variabelen niet dezelfde waarheidswaarde hebben, dan is de hele premisse onwaar.
- In de vierde regel staat dat ‘p ↔ q’, het regent dan en slechts dan als de straat nat is, waar is wanneer zowel ‘p’ als ‘q’ onwaar zijn. Dus ‘p ↔ q’ is waar als het niet regent en de straat niet nat is. Als beide variabelen onwaar zijn, is de hele premisse waar.
→
De laatste waarheidstafel die wij moeten behandelen is die van de logische constante ‘→’, als.., dan… In het voorbeeld is p = het regent en q = de straat is nat, de uitspraak is dus ‘als het regent dan is de straat nat‘:
- Hier staat in de eerste regel dat ‘p → q’ waar ‘w’ is als zowel ‘p’ als ‘q’ afzonderlijk ook waar ‘w’ zijn. Dus het regent en de straat is nat. Als ze beiden waar zijn, dan is de hele premisse ook waar.
- In de tweede regel staat dat ‘p → q’, als het regent, dan is de straat nat, onwaar is wanneer ‘p’ waar is en ‘q’ onwaar. Dus ‘p → q’ is onwaar als het wel regent, maar de straat niet nat is. De oorzaak ‘p’ is er wel, maar het gevolg ‘q’ niet en dat kan niet. Volgens de premisse kan het niet zo zijn dat het wel regent, maar de straten niet nat worden.
- In de derde regel staat dat ‘p → q’, als het regent, dan is de straat nat, waar is wanneer ‘p’ onwaar is en ‘q’ waar. Dus ‘p → q’ is waar als het niet regent en de straat nat is. De hele premisse kan nog wel waar zijn, ondanks dat deze ene oorzaak er niet is. Het gevolg, de natte straten, zou een andere oorzaak kunnen hebben.
- In de vierde regel staat dat ‘p → q’, als het regent, dan is de straat nat, waar is wanneer zowel ‘p’ als ‘q’ onwaar is. Dus ‘p → q’ is waar als het niet regent en de straat niet nat is. Als beide variabelen onwaar zijn, dan kan de premisse wel waar zijn. Als het niet regent en de straten niet nat zijn, dan kan de hele premisse (als het regent, dan is de straat nat) nog wel waar zijn.
De waarheidstafels zijn een manier om de geldigheid van een argumentatie te bepalen. Er zijn vijf basiswaarheidstafels, van elke logische constante één. Voor een waarheidstafel van een hele argumentatie moet je soms meerdere basiswaarheidstafels samenvoegen. Oftewel waarheidstafels 2.0.